- महत्वपूर्ण लेख
- सामान्य सवाल
फैक्टोरियल: n! को ‘n फैक्टोरियल’ के रूप में पढ़ा जाता है, जहाँ n एक पूर्ण संख्या या (गैर ऋणात्मक संख्या) है और
n! = n × (n – 1) × (n – 2) … × 3 × 2 × 1
उदाहरण
- 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
- 5! = 5 × 4 × 3 × 2 × 1
- 11! = 11 × 10 × 9 × 8!
- 1! = 1 = 0!
- 8! + 5! = 8 × 7 × 6 × 5! + 5! = 5! × (8 × 7 × 6 + 1) = 5! × 337
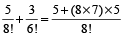 [नोट: a! और b! का LCM a! होगा, यदि a > b]
[नोट: a! और b! का LCM a! होगा, यदि a > b]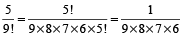
- 5! ×3! ≠ 15!
गणना के मूल सिद्धांत (Fundamental Principles of Counting)
योगफल सिद्धांतः यदि एक संक्रिया (operation) ‘m’ विभिन्न तरीकों से की जा सकती है तथा दूसरी संक्रिया जो पहली संक्रिया पर निर्भर नहीं है, को ‘n’ विभिन्न तरीकों से किया जा सकता है, तो उनमें से किसी एक संक्रिया को कुल (m + n) तरीकों से किया जा सकता है।
गुणनफल का सिद्धांतः यदि एक संक्रिया (operation) ‘m’ विभिन्न तरीकों से की जा सकती है तथा इसके बाद दूसरी संक्रिया ‘n’ विभिन्न तरीकों से की जा सकती है तो दोनों संक्रियाओं को एक साथ कुल (m × n) तरीकों से किया जा सकता है।
क्रमचय (Permutations)
किसी दिए गए वस्तुओं के समूह में से कुछ अथवा सभी वस्तुएँ लेकर बनाया गया विन्यास या व्यवस्था उस समूह का एक क्रमचय कहलाता है।
संचय (Combinations)
दी गई वस्तुओं में से कुछ अथवा सभी को एक साथ लेकर क्रम का ध्यान u रखते हुए जो भिन्न-भिन्न समूह बनाए जाते हैं उन्हें उन वस्तुओं का संचय कहते हैं।
क्रमचय और संचय में अंतर (Difference between Permutation and Combination)
क्रमचय एवं संचय में अंतर को समझने के लिए हम निम्नलिखित उदाहरण पर विचार करते हैं-
4 वस्तुएँ A, B, C और D में से तीन वस्तुओं का संभव चुनाव (या संचय) और सजाना (या क्रमचय) निम्न प्रकार से होगा:
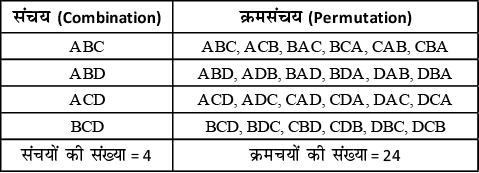
क्रमचय के लिए गणना सूत्र (Number of permutations of N elements)
n विभिन्न वस्तुओं में से एक बार में सभी वस्तुऐं लेकर बनाए गए क्रमचयों की संख्या, जहाँ पुनरावृत्ति नहीं होती है।
n × (n – 1) … × 4 × 3 × 2 × 1 = n!
उदाहरण 1. शब्द KUMAR के अक्षर को अलग-अलग कितनी तरह से क्रमबद्ध किए जा सकते है?
- 360
- 120
- 220
- 500
हल: (2) शब्द KUMAR में 5 विभिन्न अक्षर हैं।
अतः क्रमचयों की संख्या = 5! = 5 × 4 × 3 × 2 × 1 = 120
उदाहरण 2. शब्द BIJENDRA के अक्षर कितने प्रकार से सजाए जा सकते हैं?
- 90
- 6050
- 180
- 40320
हल: (4) शब्द BIJENDRA में 8 विभिन्न अक्षर हैं।
अतः क्रमचयों की संख्या = 8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40320
n विभिन्न वस्तुओं में से एक बार में ‘r‘ वस्तुएँ लेकर बनाए गए कुल क्रमचयों की संख्या, जहाँ पुनरावृत्ति नहीं होती है, को nPr से व्यक्त करते हैं। तब:
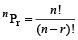 , जहाँ 0 ≤ r ≤ n
, जहाँ 0 ≤ r ≤ n
उदाहरण 3. शब्द MOHAN के अक्षरों में से तीन अक्षरों को अलग-अलग कितनी तरह से क्रमबद्ध किए जा सकते है?
- 60
- 6050
- 180
- 40320
हल: (1) शब्द MOHAN में 5 विभिन्न अक्षर हैं।
अतः क्रमचयों की संख्या = 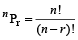
= 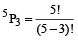 =
= 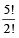 = 5 × 4 × 3 = 60
= 5 × 4 × 3 = 60
यदि n वस्तुओं में से p वस्तुएँ एक प्रकार की, q वस्तुएँ दूसरे प्रकार की, r वस्तुएँ तीसरे प्रकार की हों, तथा शेष वस्तुएँ भिन्न-भिन्न प्रकार की हों, तब सभी n वस्तुओं को एक साथ लेकर बने क्रमचयों की संख्या 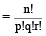
उदाहरण 4. शब्द SULTANGANJ के अक्षरों से कितने शब्द बनाये जा सकते हैं?
- 11000
- 10080
- 907200
- 14000
हल: (3) शब्द SULTANGANJ में कुल 10 अक्षर हैं, जिसमें A और N दो-दो बार आते हैं।
∴ अभीष्ट संख्या = 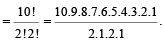 = 907200
= 907200
उदाहरण 5. क्रमचयों और संचयों की संख्या ज्ञात करें।
n = 6, r = 4.
हल:
स्टेप 1: 6 का फेक्टोरियल ज्ञात करें।
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
स्टेप 2: 6 – 4 का फेक्टोरियल ज्ञात करें।
(6-4) ! = 2! = 2
स्टेप 3: 720 को 2 से विभाजित करें।
क्रमचय = 720/2 = 360
स्टेप 4: 4 का फेक्टोरियल ज्ञात करें।
4! = 4 × 3 × 2 × 1 = 24
स्टेप 5: 360 को 24 से विभाजित करें।
संचय = 360/24 = 15
उदाहरण 6. किसी कक्षा में 10 लड़के और 8 लड़कियाँ हैं। कक्षा-शिक्षक मोनिटर के पद के लिए एक विद्यार्थी का चुनाव करना चाहता है। कितने प्रकार से कक्षा-शिक्षक यह चुनाव कर सकता है?
हल: शिक्षक, मोनिटर पद के लिए विद्यार्थी का चुनाव दो प्रकार से कर सकता हैः
- 10 लड़कों में एक लड़के का चुनाव 10 प्रकार से किया जा सकता है, या
- 8 लड़कियों में एक लड़की का चुनाव 8 प्रकार से किया जा सकता है।
अतः योग के मौलिक सिद्धांत से, या तो एक लड़का या एक लड़की का 10 + 8 = 18 प्रकार से चुनाव किया जा सकता है।
उदाहरण 7. एक कक्षा में 10 लड़के और 8 लड़कियाँ है। शिक्षक कक्षा का प्रतिनिधित्व करने के लिए एक लड़का और एक लड़की का चुनाव करना चाहता है। कितने प्रकार से शिक्षक यह चुनाव कर सकता है?
हल: शिक्षक इसे निम्नलिखित दो प्रकार से कर सकता हैः
- 10 लड़कों में एक लड़के का चुनाव 10 प्रकार से किया जा सकता है
- 8 लड़कियों में एक लड़की का चुनाव 8 प्रकार से किया जा सकता है।
अभीष्ट प्रकार = 10 × 8 = 80
उदाहरण 8. ABCD के सभी अक्षरों के क्रमचयों की सूची बनायें।
हल:
| ABCD | ABDC | ACBD | ACDB | ADBC | ADCB |
| BACD | BADC | BCAD | BCDA | BDAC | BDCA |
| CABD | CADB | CBAD | CBDA | CDAB | CDBA |
| DABC | DACB | DBAC | DBCA | DCAB | DCBA |
यहाँ हम क्रमचयों की संख्या निकालने वाले सूत्र का उपयोग करेंगे।
जहाँ पर चार वस्तुएँ हों और एक बार में 4 का चयन करना हो, तो
⁴P₄ = 4!/(4 – 4) ! = 4!/0! = 24/1 = 24
उदाहरण 9. शब्द HAND में तीन अक्षरों के सभी क्रमचयों की सूची बनायें।
हल:
| HAN | HNA | HAD | HDA | HND | HDN |
| AHN | ANH | AHD | ADH | AND | ADN |
| NHD | NDH | NAH | NHA | NAD | NDA |
| DHA | DAH | DAN | DNA | DHN | DNH |
यहाँ हम क्रमचयों की संख्या निकालने वाले सूत्र का उपयोग करेंगे।
जहाँ पर 4 वस्तुएँ हों और एक बार में 3 का चयन करना हो, तो
⁴P₃ = 4!/(4 – 3) ! = 4!/1! = 24/1 = 24.
उदाहरण 10. एक वृत्तीय टेबल के चारों ओर किसी स्कूल के 6 विद्यार्थी कितने प्रकार से बैठ सकते हैं?
हल: यह चक्रीय क्रमचय पर आधारित प्रश्न है।
6 विद्यार्थियों के बैठने का प्रकार = 1 × (6 – 1) !
5! = 5 × 4 × 3 × 2 × 1 = 120
उदाहरण 11. 1 से 7 के अंकों का उपयोग कर चार अंकों वाली कितनी संख्याएँ (बिना दोहराये) बनायी जा सकती है यदि 4 सभी संख्याओं में शामिल हों?
हल: कुल अंक (n) = 7
संख्या निर्माण के कुल तरीके यदि 4 सभी में शामिल हों
= r × n-1Pr-1 = 4 × ⁶P₃ = 480
उदाहरण 12. शब्द BANANA के अक्षरों को कितने भिन्न-भिन्न तरीके से लिखा जा सकता हैं?
हल: इस शब्द में छः अक्षर हैं जिसमें से तीन A, दो N और एक B है। इसलिए अक्षरों को लिखने के भिन्न-भिन्न तरीके हैंः
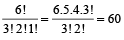
उदाहरण 13. 5 स्वरों का उपयोग कर 3 अक्षर वाले कितने भिन्न-भिन्न शब्द बनाये जा सकते हैं, यदि A उसमें शामिल नहीं हों?
हल: कुल अक्षर (n) = 5
इसलिए कुल तरीके = n-1Pr = 5-1P3 = ⁴P₃ = 24
उदाहरण 14. कितने प्रकार से हम पाँच स्वरों a, e, i, o और u को व्यवस्थित कर सकते हैं यदि:
(i) दो स्वर e और i हमेशा एक साथ रहें।
(ii) दो स्वर e और i कभी भी एक साथ नहीं रहे।
हल: (i) सूत्र m!(n – m + 1) !
यहाँ n = 5, m = 2(e – i)
⇒ अभीष्ट प्रकार की संख्या = 2!(5 – 2 + 1) ! = 2 × 4! = 48
(ii) जब e और i कभी भी एक साथ नहीं हैं के प्रकारों की संख्या
= 5 स्वरों को व्यवस्थित करने के कुल प्रकारों की संख्या
= 5! – 48 = 72
या n! – m!(n – m + 1) ! = 5! – 48 = 72
उदाहरण 15. शब्द MISSISSIPPI के अक्षरों से कितने भिन्न-भिन्न शब्द बनाए जा सकते हैं?
हल: शब्द MISSISSIPPI में 4I, 4S और 2P
अतः अभीष्ट शब्दों की संख्या = 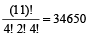
उदाहरण 16. कितने तरीके से 5 पुरस्कारों को 4 लड़कों में वितरित किया जा सकता है जब प्रत्येक लड़का सभी पुरस्कारों को लेने योग्य है?
हल: कोई भी एक पुरस्कार 4 तरीके से दिया जा सकता है तब शेष 4 पुरस्कारों में कोई भी एक पुरस्कार पुनः चार तरीकों से दिया जा सकता है।
इस तरह से, 5 पुरस्कारों को 4 × 4 × 4 × 4 × 4 = 4⁵ तरीके से दिया जा सकता है।
उदाहरण 17. कितने प्रकार से 16 खिलाड़ियों में से 11 खिलाड़ियों का एक हाॅकी टीम बनाया जा सकता है?
हल: कुल प्रकारों की संख्या = 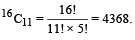
= 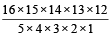 = 4368.
= 4368.
उदाहरण 18. एक शतरंज के बोर्ड से कितने वर्ग बनाये जा सकते हैं?
हल: एक शतरंज का बोर्ड 9 बराबर भागों वाले ऊर्ध्वाधर और क्षैतिज रेखाओं से बना होता है। 1 × 1 वर्ग बनाने के लिए हमें दी गई रेखाओं में से दो क्रमागत ऊर्ध्वाधर और क्षैतिज रेखाओं को चुनना होगा। यह 8 × 8 = 8² प्रकार से चुना जा सकता है।
एक 2 × 2 वर्ग के लिए तीन क्रमागत ऊर्ध्वाधर और क्षैतिज रेखाओं की जरूरत होती है और इसे हम 7 × 7 = 7² प्रकार से कर सकते है।
इस तरह से, कुल वर्गो की संख्या = 8² + 7² +6² … +2² + 1²
= 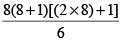 = 204.
= 204.
स्मरणीय तथ्य (Points to Remember)

0! = 1
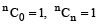 ;
; 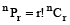
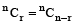
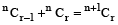
nCx = nCy ⇒ x + y = n
nCr = nCr+1= n+1Cr
nCr = 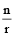 – n-1Cr-1
– n-1Cr-1
nCr = 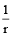 (n – r + 1) nCr-1
(n – r + 1) nCr-1
nC1 = nCn-1 = n
